Configure LinearDiscriminantAnalysis "n_components" Parameter

The n_components parameter in scikit-learn’s LinearDiscriminantAnalysis controls the number of components for dimensionality reduction.

Linear Discriminant Analysis (LDA) is a method used for classification and dimensionality reduction. It projects the data onto a lower-dimensional space while maximizing the separability between classes.

The n_components parameter determines the number of components to keep after the LDA transformation. It affects the model’s ability to capture class distinctions and can impact classification performance.

By default, n_components is set to min(n_classes - 1, n_features), where n_classes is the number of target classes and n_features is the number of input features.

In practice, values ranging from 1 to min(n_classes - 1, n_features) are commonly used, depending on the dataset’s characteristics and the desired trade-off between dimensionality reduction and class separability.

from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.metrics import accuracy_score
import numpy as np
import matplotlib.pyplot as plt

# Generate synthetic dataset
X, y = make_classification(n_samples=1000, n_features=20, n_informative=15,
                           n_redundant=5, n_classes=5, random_state=42)

# Split into train and test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Train with different n_components values
n_components_range = range(1, 5)  # 5 classes, so max n_components is 4
accuracies = []

for n in n_components_range:
    lda = LinearDiscriminantAnalysis(n_components=n)
    lda.fit(X_train, y_train)
    X_train_lda = lda.transform(X_train)
    X_test_lda = lda.transform(X_test)

    # Train a new LDA classifier on the transformed data
    lda_clf = LinearDiscriminantAnalysis()
    lda_clf.fit(X_train_lda, y_train)
    y_pred = lda_clf.predict(X_test_lda)

    accuracy = accuracy_score(y_test, y_pred)
    accuracies.append(accuracy)
    print(f"n_components={n}, Accuracy: {accuracy:.3f}")

# Plot accuracy vs n_components
plt.plot(n_components_range, accuracies, marker='o')
plt.xlabel('n_components')
plt.ylabel('Accuracy')
plt.title('LDA Performance vs n_components')
plt.show()

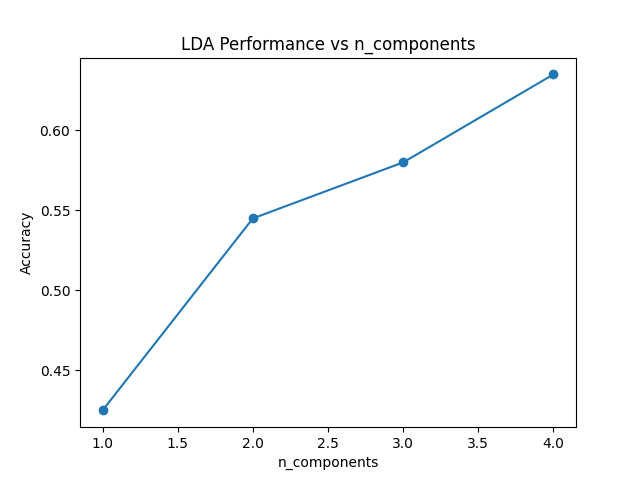
Running the example gives an output like:

n_components=1, Accuracy: 0.425
n_components=2, Accuracy: 0.545
n_components=3, Accuracy: 0.580
n_components=4, Accuracy: 0.635

Configure LinearDiscriminantAnalysis “n_components” Parameter

The key steps in this example are:

Generate a synthetic multi-class dataset with informative and redundant features
Split the data into train and test sets
Train LinearDiscriminantAnalysis models with different n_components values
Transform the data using LDA and train a classifier on the transformed data
Evaluate the accuracy of each model on the test set
Visualize the relationship between n_components and classification accuracy

Tips for setting n_components:

Start with the default value and experiment with lower values to find the optimal trade-off between dimensionality reduction and classification performance
Consider the number of classes in your dataset, as n_components cannot exceed n_classes - 1
Examine the explained variance ratio to determine how much information is retained by each component

Issues to consider:

Using too few components may result in loss of important class-discriminating information
Using too many components may lead to overfitting, especially with small datasets
The optimal n_components value depends on the specific characteristics of your dataset and the problem you’re trying to solve

See Also