Configure ExtraTreesRegressor "ccp_alpha" Parameter

The ccp_alpha parameter in scikit-learn’s ExtraTreesRegressor controls the complexity of the trees through cost-complexity pruning.

Extra Trees Regressor is an ensemble method that builds multiple randomized decision trees and averages their predictions. The ccp_alpha parameter sets the complexity parameter for Minimal Cost-Complexity Pruning.

Increasing ccp_alpha leads to more pruning, which can help reduce overfitting by removing branches that provide little predictive power. This often results in simpler, more interpretable trees at the cost of some predictive accuracy.

The default value for ccp_alpha is 0.0, which means no pruning is performed.

In practice, values are typically small, often ranging from 0.001 to 0.05, depending on the specific dataset and problem.

import numpy as np
from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split
from sklearn.ensemble import ExtraTreesRegressor
from sklearn.metrics import mean_squared_error
import matplotlib.pyplot as plt

# Generate synthetic dataset
X, y = make_regression(n_samples=1000, n_features=10, noise=0.1, random_state=42)

# Split into train and test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Train with different ccp_alpha values
ccp_alpha_values = [0.0, 0.001, 0.01, 0.05, 0.1]
mse_scores = []

for alpha in ccp_alpha_values:
    etr = ExtraTreesRegressor(n_estimators=100, random_state=42, ccp_alpha=alpha)
    etr.fit(X_train, y_train)
    y_pred = etr.predict(X_test)
    mse = mean_squared_error(y_test, y_pred)
    mse_scores.append(mse)
    print(f"ccp_alpha={alpha:.3f}, MSE: {mse:.3f}")

# Plot results
plt.figure(figsize=(10, 6))
plt.plot(ccp_alpha_values, mse_scores, marker='o')
plt.xscale('log')
plt.xlabel('ccp_alpha')
plt.ylabel('Mean Squared Error')
plt.title('Effect of ccp_alpha on ExtraTreesRegressor Performance')
plt.show()

Running the example gives an output like:

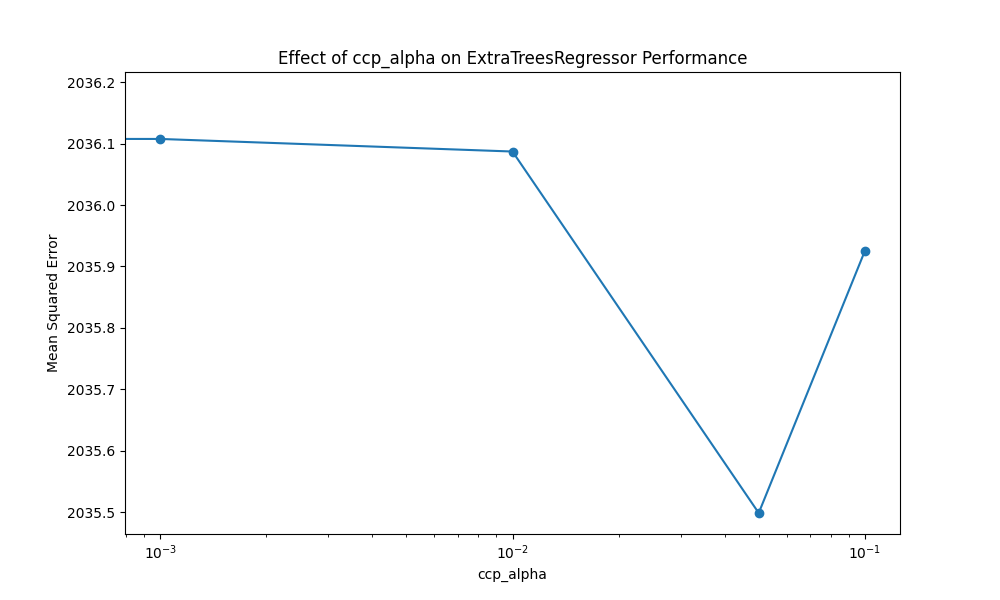
ccp_alpha=0.000, MSE: 2036.183
ccp_alpha=0.001, MSE: 2036.108
ccp_alpha=0.010, MSE: 2036.087
ccp_alpha=0.050, MSE: 2035.498
ccp_alpha=0.100, MSE: 2035.925

Configure ExtraTreesRegressor “ccp_alpha” Parameter

The key steps in this example are:

Generate a synthetic regression dataset
Split the data into train and test sets
Train ExtraTreesRegressor models with different ccp_alpha values
Evaluate the mean squared error of each model on the test set
Plot the relationship between ccp_alpha and model performance

Some tips and heuristics for setting ccp_alpha:

Start with small values (e.g., 0.001) and gradually increase
Use cross-validation to find the optimal value for your specific dataset
Monitor the trade-off between model complexity and performance
Consider using ccp_alpha in combination with other regularization techniques

Issues to consider:

Higher ccp_alpha values lead to simpler trees but may reduce predictive accuracy
The optimal ccp_alpha depends on the complexity of the underlying relationship in the data
Pruning can significantly impact model interpretability and feature importance
There may be interactions between ccp_alpha and other hyperparameters like max_depth

See Also