Configure BaggingRegressor "n_estimators" Parameter

The n_estimators parameter in scikit-learn’s BaggingRegressor controls the number of base estimators in the ensemble.

Bagging is an ensemble method that combines predictions from multiple base estimators to reduce overfitting and improve model stability. The n_estimators parameter determines how many base estimators are created and used in the ensemble.

Increasing the number of estimators generally improves the model’s performance by reducing variance. However, there’s a trade-off between performance and computational cost, with diminishing returns as n_estimators increases.

The default value for n_estimators in BaggingRegressor is 10.

In practice, values between 10 and 100 are commonly used, depending on the dataset’s size and complexity, and the computational resources available.

from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split
from sklearn.ensemble import BaggingRegressor
from sklearn.metrics import mean_squared_error
import numpy as np
import matplotlib.pyplot as plt

# Generate synthetic dataset
X, y = make_regression(n_samples=1000, n_features=20, noise=0.1, random_state=42)

# Split into train and test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Train with different n_estimators values
n_estimators_values = [1, 5, 10, 20, 50, 100]
mse_scores = []

for n in n_estimators_values:
    bgr = BaggingRegressor(n_estimators=n, random_state=42)
    bgr.fit(X_train, y_train)
    y_pred = bgr.predict(X_test)
    mse = mean_squared_error(y_test, y_pred)
    mse_scores.append(mse)
    print(f"n_estimators={n}, MSE: {mse:.3f}")

# Plot results
plt.plot(n_estimators_values, mse_scores, marker='o')
plt.xscale('log')
plt.xlabel('n_estimators')
plt.ylabel('Mean Squared Error')
plt.title('Effect of n_estimators on BaggingRegressor Performance')
plt.show()

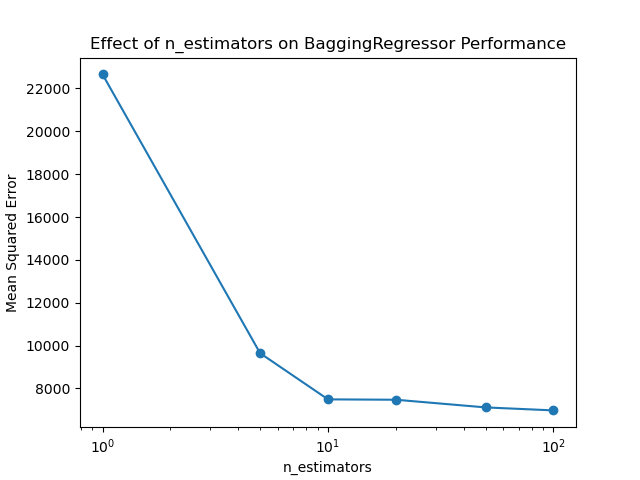
Running the example gives an output like:

n_estimators=1, MSE: 22658.256
n_estimators=5, MSE: 9641.348
n_estimators=10, MSE: 7486.481
n_estimators=20, MSE: 7469.022
n_estimators=50, MSE: 7111.178
n_estimators=100, MSE: 6971.395

Configure BaggingRegressor “n_estimators” Parameter

The key steps in this example are:

Generate a synthetic regression dataset with multiple features
Split the data into train and test sets
Train BaggingRegressor models with different n_estimators values
Evaluate the Mean Squared Error (MSE) of each model on the test set
Visualize the relationship between n_estimators and model performance

Some tips and heuristics for setting n_estimators:

Start with the default value of 10 and increase it until performance plateaus
Consider the trade-off between model performance and computational cost
For smaller datasets, a lower number of estimators may be sufficient

Issues to consider:

The optimal number of estimators depends on the dataset’s size and complexity
Using too few estimators may result in underfitting, while too many can be computationally expensive
The performance gain often diminishes as the number of estimators increases
Ensure you have sufficient computational resources when using a large number of estimators

See Also