Scikit-Learn power_transform() for Data Preprocessing

Power transformation is a technique used to stabilize variance, make the data more Gaussian-like, and improve the performance of downstream algorithms.

The power_transform() function in scikit-learn can apply either a Box-Cox or Yeo-Johnson transformation to the data.

This transformation is particularly useful for data preprocessing in regression and classification tasks where the features do not follow a normal distribution.

from sklearn.datasets import make_regression
from sklearn.preprocessing import power_transform
import matplotlib.pyplot as plt
import numpy as np

# generate regression dataset
X, y = make_regression(n_samples=100, n_features=1, noise=0.1, random_state=1)
X = np.exp(X)  # add skewness to the distribution

# plot before transformation
plt.subplot(1, 2, 1)
plt.hist(X, bins=30)
plt.title('Before Power Transform')

# apply power transform
X_transformed = power_transform(X, method='yeo-johnson')

# plot after transformation
plt.subplot(1, 2, 2)
plt.hist(X_transformed, bins=30)
plt.title('After Power Transform')

plt.show()

Running the example gives an output like:

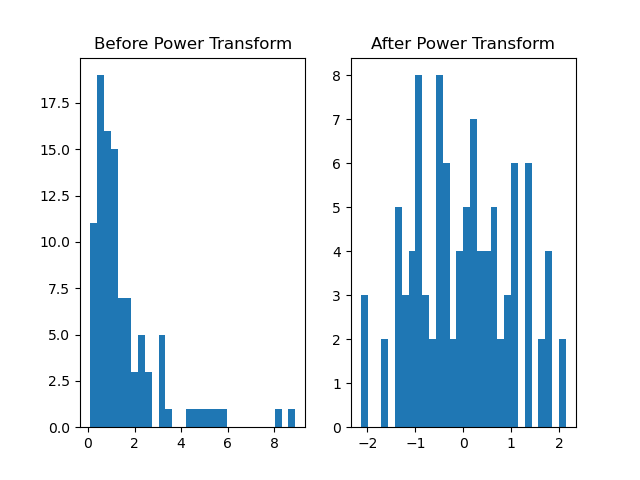
The steps are as follows:

1. First, generate a synthetic regression dataset using make_regression(). This creates a dataset with a specified number of samples (n_samples), features (n_features), and a fixed random seed (random_state) for reproducibility.

2. Plot the distribution of the dataset before applying the transformation using matplotlib.

3. Apply the power_transform() function to the dataset, specifying the method parameter as 'yeo-johnson'.

4. Plot the distribution of the dataset after applying the transformation using matplotlib to visually assess the changes.

This example demonstrates how to use power_transform() to preprocess data by stabilizing variance and making the data more Gaussian-like, which can improve the performance of downstream machine learning algorithms.