SKLearner Home | About | Contact | Examples

Scikit-Learn KernelDensity Model

How to Use KernelDensity

KernelDensity is a non-parametric method for estimating the probability density function of a dataset.

The key hyperparameters include bandwidth (the width of the kernel) and kernel (the type of kernel function, e.g., ‘gaussian’).

This algorithm is suitable for density estimation and can be applied to anomaly detection, data generation, and more.

from sklearn.neighbors import KernelDensity
import numpy as np
import matplotlib.pyplot as plt

# generate synthetic dataset
X = np.random.normal(0, 1, 1000)[:, np.newaxis]

# fit KernelDensity model
kde = KernelDensity(kernel='gaussian', bandwidth=0.5).fit(X)

# evaluate the density model on the data
X_plot = np.linspace(-5, 5, 1000)[:, np.newaxis]
log_dens = kde.score_samples(X_plot)

# plot the estimated density
plt.fill_between(X_plot[:, 0], np.exp(log_dens), alpha=0.5)
plt.plot(X[:, 0], -0.01 - 0.05 * np.random.random(X.shape[0]), '+k')
plt.title('Kernel Density Estimation')
plt.show()

# make a density estimate for a sample
sample = [[0.5]]
log_density = kde.score_samples(sample)
print('Log Density Estimate for sample:', log_density[0])

Running the example gives an output like:

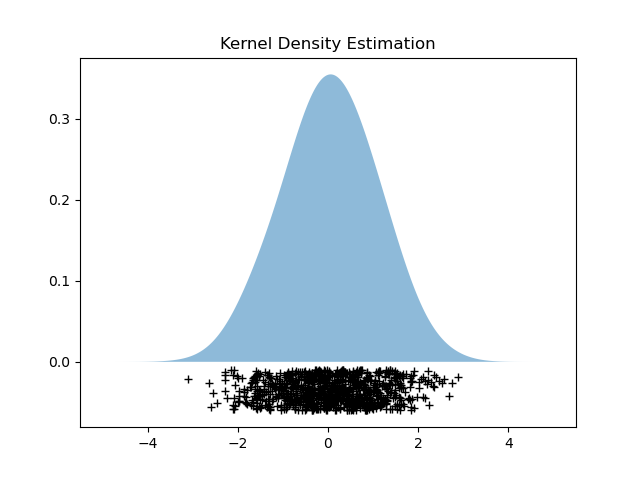
Scikit-Learn KernelDensity

The steps are as follows:

  1. Generate a synthetic dataset using numpy with 1000 samples drawn from a normal distribution. Each sample is reshaped to have one feature.
  2. Fit a KernelDensity model using a Gaussian kernel and a bandwidth of 0.5.
  3. Evaluate the density model by scoring a range of values from -5 to 5, which provides the log of the estimated density for each point.
  4. Plot the estimated density function. The data points are plotted along the x-axis with jitter to show their distribution.
  5. Make a density estimate for a specific sample and print the log of the estimated density.

This example demonstrates how to use KernelDensity for probability density estimation, showcasing the steps to fit the model and visualize the estimated density function. The model can be used to estimate densities for new samples, providing insights into the distribution of the data.



See Also